Vector Network: Core Concepts and Terminology
This document defines the key mathematical and structural concepts used in the VectorNetwork model for representing vector graphics.
Overview
- A Vector Network is a graph-based structure for 2D vector shapes.
- It generalizes SVG
<path>data with explicit support for multiple subpaths, compound shapes, holes, and both linear and Bézier segments. - The core components are: vertices, segments, loops, regions, and fill rules.
Vertices
- Vertex: A point in 2D space, defined as
(x, y) ∈ ℝ². - Vertices are indexed by position in the
verticeslist. - All segments reference vertices by their indices.
Segments
- Segment: An edge connecting two vertices, possibly with Bézier control tangents.
- Defined by:
a: start vertex indexb: end vertex indexta: (optional) tangent vector at start vertex (for Bézier control)tb: (optional) tangent vector at end vertex (for Bézier control)
- Defined by:
- Types:
- Linear: if both tangents are zero or omitted.
- Cubic Bézier: if either tangent is nonzero.
- Segments are directed (from
atob).
Loops
- Loop: A closed, ordered sequence of segment indices forming a contiguous path (contour) that starts and ends at the same vertex.
- Each loop must be topologically closed (forms a ring).
- Analogous to a "subpath" or a single closed shape in SVG.
Regions
- Region: A filled area defined by one or more loops.
- The first loop: defines the outer boundary ("positive" area).
- Subsequent loops: define holes ("negative" areas) inside the region.
- A region may represent:
- A simple shape (single loop, no holes)
- A compound shape with holes (multiple loops)
- Disjoint islands (multiple regions)
Fill Rules
- Fill Rule: Determines how overlapping loops and holes combine to define filled areas.
- EvenOdd: A point is inside the region if it crosses an odd number of loops (parity rule).
- NonZero: A point is inside if the sum of winding numbers (directional crossings) ≠ 0.
- Fill rules affect how compound shapes and holes are rendered.
Planar vs Nonplanar Networks
- Planar Network: All segments and vertices lie in a single 2D plane, and no segments cross except at shared vertices.
- Nonplanar Network: The graph may have crossing segments (not embeddable in the plane without intersections), which can lead to ambiguous or undefined regions.
- The
VectorNetworkmodel is primarily intended for planar networks, but does not enforce planarity.
Implicit Regions
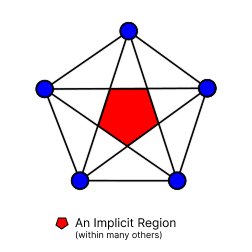
- If no explicit regions are defined:
- The network is interpreted as a set of open or closed paths (for stroking or outline rendering).
- No fill is applied; only the connectivity of segments is used.
- If regions are defined:
- Only areas described by the regions and their fill rules are considered filled.